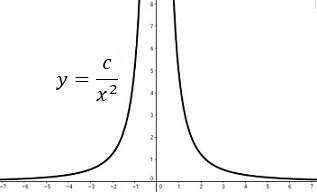
Introducción al cálculo diferencial.
El cálculo constituye la matemática del cambio, sus aplicaciones tracienden mucho más allá de las matemáticas, adentrandose al mundo de las ciencias como son la física, química, economía, estadística entre otras.
El cálculo proporciana herramientas para la explicación de muchos cuestionamientos científicos de gran relavacia para la humanidad que matemáticamente resultaría muy tediosos de realizar solo con el uso del algebra y/o geometría.
Para su mejor estudio y comprensión el cálculo está dividido en cálculo diferencial, cálculo integral, cálculo vectorial, ecuaciones diferenciales y cálculo de variables complejas.
El cálculo diferencial constituye la matemática del cambio. Trata el análisis matemátematico del cambio infinitesimal en las funciones de estudio basádo en la operación matemática conocida como la diferenciación (determinación de la derivada de una función).
Su estudio comienza con el concepto del límite de una función, el analisis de la continuidad, da respuesta a uno de los cuestionamientos más antiguos en matemática el problema de la recta tangente a una curva, estudia los valores mínimos o máximos, los comportamientos de una variable que esta cambiando respecto a otra "razones de cambio relacionadas", por ejemplo como cambia la temperatura de un objeto o cuerpo al pasar el tiempo segun el medio, hasta profundizar en el análisis gráficos de los sucesos relacionados a las funciones reales, entre otras cosas.
Como prerequisitos para iniciar con el estudio del cálculo conviene y es necesario recordar algunos conceptos relacionados a las funciones reales, muy especialmente el concepto de dominio, el cual posee una gran relavancia de suma en las matemáticas del cambio.
En adición al conocimiento relacionado a las funciones algebraicas, el estudiante debe poseer un buen manejo algebraico de temas como factorización, división sintética, y racionalización, estos sirven de base para el cálculo de límites analíticos, el cual es el primer acercamiento del estudiante y el cálculo.
Límite: conceptos fundamentales.
Concepto de límite.
Imagine que coloca un balde vacío debajo de un grifo de agua el cual vierte un pequeño chorro de agua en el balde continuamente, hasta que el balde se llena. Ahora usted toma un jarro y comienza a sacar el agua que está en balde, con tal rapidez que este comienza a vaciarse debido a que no está entrando agua con la misma rapidez a la que sale. ¿Existe algún instante en el cual la cantidad de agua en el balde sea cero? ¿Es posible continuar por tiempo prologando, extrayendo el agua del balde sin detenerse?
Note que, aunque el agua en el balde nunca es cero, para usted existe un momento en el cual coloquialmente se dice que la cantidad de agua en el balde es cero, debido a que eventualmente habrá un instante en el cual tendrá que detenerse y esperar que el vuelva a haber una cantidad considerable de agua para así poder seguir extrayendo. En el instante en que solo existe en el balde una gota de agua (o menos) se dice que la cantidad de agua tiende a cero (se acerca a cero, pero no lo es).
Por otra parte, imagine que intenta pasar desde un dormitorio de la casa hasta otro, sin pasar por la puerta. Al comenzar a caminar en dirección hacia una pared usted llegaría hasta un punto cercano a la pared, se acercará tanto como sea posible, pero no llegará a estar en el lugar de la pared, ni mucho menos podrá llegar al otro dormitorio de la casa.
Definición informal del límite.
Si \(f\left(x\right)\) se acerca arbitrariamente al mismo número \(L\) cuando \(x\) se aproxima a \(c\) por la izquierda y la derecha, entonces el límite de \(f\left(x\right)\) cuando se aproxima \(c\) es \(L\), lo cual se escribe, $$\lim_{x \to c}{f\left(x\right)}=L$$ Lo cual se lee como "límite cuando equis tiende a \(c\) de efe de equis es \(L\)". Esto es la existencia del límite está condicionada a que a medida que se aproxime tanto como se quiera la variable independiente al valor \(c\), la función se acerque tanto por la izquierda como por la derecha al mismo número \(L\).
Para determinar el límite de una función existen tres métodos fundamentales, tablas, gráficas y manejo analítico. Dichos métodos se presentan con detalles en las pestañas de arriba correspondiente al contenido de cada tema.
Para más contenidos y luego clic en la pestaña del contenido deseado.
Límites por aproximación (tablas).
El homólogo matemático para el concepto de límite se obtine al evaluar una función cualquiera \(f\left(x\right)\) para un determinado valor \(c\) dentro de su dominio, se obtiene un valor \(f\left(c\right),\) el cual está dentro del codominio (rango) de la función.
¿Sin embargo, qué pasaría si una función no existe para un valor \(c\) y existe para valores inmediatamente a la izquierda y a la derecha de dicho valor? ¿Qué expresaría este resultado sobre la función?
Como primer contacto en la determinación de límites matemático se presenta el método tabular (por tablas), el mismo consiste en evaluar la función dada en valores cercanos por la izquierda y la derecha al valor en el cual se desea determinar el límite, para luego construir una tabla de valores que permita inferir si existe o no el límite en el punto de análisis, como se muestra continuación.
Suponga que se le pide investigar el comportamiento de la función racional, $$f\left(x\right)=\frac{x^2-x-2}{x-2}~~~~\mathrm{donde}~~x\neq2$$ mediante la construcción de una tabla de valores en valores muy cercanos a dos, la respuesta es como sigue:


Para comprender esto y determinar la existencia o no del límite de una función en un punto determinado, analícese primero la definición informal de límites, la afirmación $$\lim_{x\to c}{f\left(x\right)}=L$$ implica dos cosas, que el límite existe y que su valor es \(L,\) pero el hecho de que el límite exista quiere decir que, límite cuando \(x\) tiende a \(c\) por la izquierda es igual al límite cuando \(x\) tiende a \(c\) por la derecha lo cual se escribe como: $$\lim_{x \to c^-}{f\left(x\right)}=\lim_{x \to c^+}{f\left(x\right)}$$ Por tanto, la existencia del límite en un punto está condicionada a que los límites laterales existan y sean iguales, esto es si, $$\lim_{x \to c^-}{f\left(x\right)}=L=\lim_{x \to c^+}{f\left(x\right).}$$ entonces, $$\lim_{x\to c}{f\left(x\right)}=L$$ Haga clic en la pestaña de Ejercicios I para ver más ejemplos resueltos de límites por aproximación mediante tablas.
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Límites de manera gráfica.
Existen varias maneras de analizar si existe o no el límite de una función además del método tabular (tablas), otra manera es mediante el análisis del comportamiento de la gráfica de la función.
Para comprender esto y determinar si existe o no el límite de una función en un punto determinado, analícese primero la definición informal de límites. La definción informal del límite $$\lim_{x\rightarrow c}{f\left(x\right)}=L$$ implica dos cosas, primero que el límite existe y luego que su valor es \(L\), pero el hecho de que el límite exista quiere decir, que el límite cuando \(x\) se tiende a \(c\) por la izquierda debe ser igual al límite cuando \(x\) tiende a \(c\) por la derecha, lo cual se escribe como $$ \lim_{x\rightarrow c^-}{f\left(x\right)}=\lim_{x\rightarrow c^+}{f\left(x\right)}$$ por tanto la existencia del límite está condicionada a que estos límites llamados límites laterales sean iguales, esto es: $$\lim_{x\rightarrow c}{f\left(x\right)}=L\ \ \Longleftrightarrow\ \ \lim_{x\rightarrow c^-}{f\left(x\right)}=\lim_{x\rightarrow c^+}{f\left(x\right)}$$ Para que el límite en un punto exista, los límites laterales deben existir y ser iguales.
Al investigar el comportamiento del límite de una función en un punto, a través del análisis de su gráfica, \(f(x)\) debe de aproximarse a \(c\) tanto como sea posible por la izquierda y la derecha siguiendo la trayectoria (línea dibujada) de dicha gráfica. Piense en la gráfica como la única carretera que lleva al destino, por lo que siempre deberá moverse a través de ella, este hecho se ilustra como sigue.
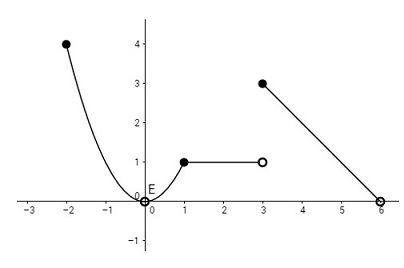
Observe detenidamente la gráfica de la función que se presenta en la parte de la izquierda y determine lo siguiente:
\(~~~a.~ f\left(-2\right)~~~~~~~b.~ f\left(0\right)~~~~~~c.~ f\left(3\right)~~~~~~\)
\begin{align}&d.~f\left(6\right)~~~~~~~e.~ \lim_{x \to 3^+}{f\left(x\right)}~~~~f.~ \lim_{x \to 1}{f\left(x\right)}~~~~~\end{align}
\begin{align}{\rm g.}~ \lim_{x\to 3}{f\left(x\right)}~~~~ &h.~ \lim_{x \to 0}{f\left(x\right)}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\end{align}
Soluciones:
\begin{array}{l}
a.~ f\left(-2\right)=4~~~~~~~~~~~~~~~~~~ &b.~ f\left(0\right)=\mathrm{no ~existe}\\
c.~ f\left(3\right)=3~~~~~~~~~~~~~~~~~~~~~ &d.~ f\left(6\right)=\mathrm{no~ existe}\end{array}
$$e.~\lim_{x \to 3^+}{f\left(x\right)}=3~~~~~~~~~~~~~~~f.~ \lim_{x \to 1}{f\left(x\right)}=1~~~~~~~$$
$$\mathrm{g.}~\lim_{x\to 3}{f\left(x\right)}= \mathrm{no~existe}~~~~ h.~\lim_{x\to 0}{f\left(x\right)}=0~~~~~~~$$
Note que cuando \(x\) tiende a tres, la función se aproxima a tres por la derecha y por la izquierda a uno, por tanto, no existe el límite.
Para ver los ejemplos resueltos y luego clic en la pestaña Ejercicios I.
Un límite que no existe. $$\mathrm{Determinar}~~~~\lim_{x \to -2} {\frac{x-2}{\left(x+2\right)\left(x-1\right)}}~~~~~~~~~~~~~~$$
Una aproximación al número de \(e.\) Demostrar que $$\lim_{x \to 0} {\left(x+1\right)^\frac{1}{x}= e ~~ \mathrm{para}~ e \approx 2.7183.}$$
Otra aoproximación para el número \(e.\) Demostrar que $$\lim_{x \to \infty} {\left(1 + \frac{1}{x}\right)^x = e~~~ \mathrm{para}~~ e \approx 2.7183}$$
Dos limites trigonometricos interesantes. Determinar mediante el uso de tablas los límites: $$\textcolor{#ff0080}{1}.\ \ \lim_{u\to 0}{\frac{\sin{u}}{u}}=1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \textcolor{#ff0080}{2}.\ \ \lim_{u\to 0}{\frac{1-\cos{u}}{u}}=0$$
Donde \(u\) es el argumento (ángulo) medido en radianes.
Análisis de gráfica. Dada la gráfica de abajo, analizar lo que se pide en cada caso.
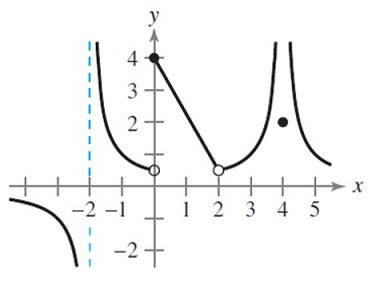 \begin{align}
&a.~f(-2)~~~~~~b.~f(2)\\
&c.~f(0)~~~~~~~~~d.~f(4)\\
&e.~\lim_{x \to -2}{f(x)}~~~~~~f.~\lim_{x \to 2}{f(x)}\\
&{\rm g.}~\lim_{x \to 0}{f(x)}~~~~~~~~h.~\lim_{x \to -4}{f(x)}
\end{align}
Calculo I Ron Larson 9th edición Ej. 26 Sección 1.2
\begin{align}
&a.~f(-2)~~~~~~b.~f(2)\\
&c.~f(0)~~~~~~~~~d.~f(4)\\
&e.~\lim_{x \to -2}{f(x)}~~~~~~f.~\lim_{x \to 2}{f(x)}\\
&{\rm g.}~\lim_{x \to 0}{f(x)}~~~~~~~~h.~\lim_{x \to -4}{f(x)}
\end{align}
Calculo I Ron Larson 9th edición Ej. 26 Sección 1.2
Un límite que no existe. Dada la gráfica de la figura abajo determine la existencia o no del límite cuando \(x\) tiende a cero.